Hypergeometric: Why Do We Play 17 Lands?
11/10/2023
"You'll be building a deck of 40 cards minimum - 23 spells and 17 lands."
If you've ever been to a casual limited event at an LGS, you've probably heard the above statement before. It's the first piece of advice told to players new to limited, presented as fact along with draft instructions and rules: there will be 3 packs; they will have 15 cards each; you will play 17 lands.
Of course, while this is a widely accepted heuristic, experienced limited players will eventually learn guidelines for when to break that heuristic.
16 lands might be good if you have a low, aggressive curve and don't want to flood out. 15 lands can even work with the lowest of curves, like many red decks in NEO.
an example trophy deck from NEO with 14 lands
18 or even 19 lands can be good for guaranteeing land drops, especially in decks with lots of mana sinks and flood protection.
an example 18-land trophy deck from STX
More and more sets recently have also been featuring nonland cards that can, in one way or another, replace lands. From
MDFCs in ZNR, to landcyclers in MOM and LTR, to Ley of the Land variants like Brave the Wilds or Bushwhack; all of these let you play fewer actual lands in your deck, while at the same time playing more effective mana sources.
an example trophy deck from WOE with 15 actual lands, plus 2 Braves and a Sprawl
These are all just vague guidelines and heuristics, and all anchored on that one original number: 17. But why? Why is 17 the right number? Very experienced limited players like myself can tell you that it certainly feels correct. But I rarely see people talking about the numbers behind this. How can we know that 17 is generally the right number, and how can we know when it isn't?
Part 1: How to Calculate
To answer the question "how many lands?", we must first consider: what are the costs and benefits of playing fewer lands, and what are the costs and benefits of playing more lands? Thankfully, the answer to both these questions are quite simple.
If we play too few lands, then the worry is mana screw. We won't be able to cast our spells, either because we don't draw enough lands, or we don't draw the right colors.
On the other hand, if we play too many lands, then the worry is mana flood. We won't have spells to cast in the first place!
Both of these concerns ask us to care about what balance of lands and spells we're drawing in the first N turns, for various values of N. Too few lands, and we get screwed. Too many, and we get flooded. And it just so happens that there's a great tool for calculating these probabilities!
Hypergeometric Calculators
It's very possible you've seen, or at least heard of hypergeometric calculators before. This is probably the most common version, and is the first result you get when googling. There's also various versions with the inputs renamed to better suit MtG players - I found a couple on Aether Hub and MTG Nexus.

standard hypergeometric calculator
But for convenience's sake, I've also coded a version on this site, which you can find in the sidebar! Simply click on the calculator icon to open it up, and feel free to use this to follow along with the calculations as you read. (this might not work well on mobile, or if you have an otherwise narrow screen)
So, first, a quick guide for those who are unfamiliar. How do you use this calculator? Well, it's quite simple. The inputs are:
- Population size: this is the number of cards you're drawing from. Generally, it will be your deck size (so 40), but if you've already drawn some cards from your deck and want to calculate stuff for the remaining portion, use the size of the remaining portion.
- Number of successes in population: this is the number of "hits" among the cards you're drawing from.
- Sample size: this is the number of cards you're drawing or otherwise looking at.
- Number of successes in sample: this is the number of "hits" you want to draw within your sample size.
So, let's say you wanted to answer the question: what are the chances I draw 2 or more of my 17 lands in my opening hand, from my deck of 40 cards? Then you would enter the following inputs, and get the following result:
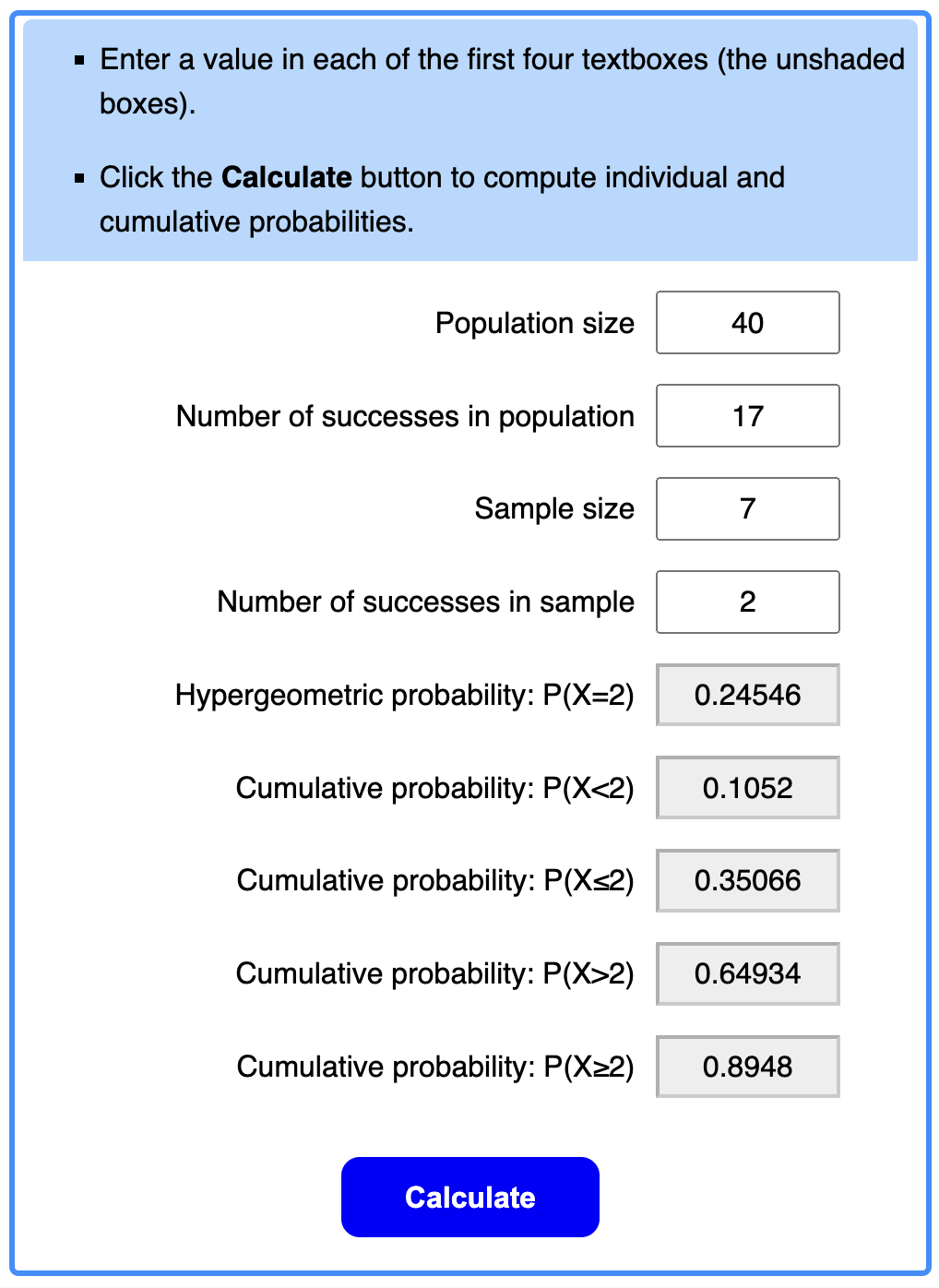
example calculation
This gives us several numbers: P(X=x) is the chance that we get exactly 2 lands, P(X≥x) is the chance we get at least 2 lands, etc. So, if the question was "chance of 2 or more lands", then the answer is about 89.5%.
Part 2: Calculating Screw
Now that we know how to use a hypergeometric calculator, we can use it to make some conclusions about land count. First up: looking at mana screw.
Disclaimer
All of the calculations I'll be doing will not be taking into account mulligans. This will mean the numbers aren't quite accurate to an exact simulation of how magic games play out - but the goal is to get intuition from estimates, not to have exact numbers to the nearest 1%.
Similarly, I will not be taking into account the Arena hand smoother. For more details on that, see Sierkovitz' excellent breakdown.
Here are two charts showing the likelihood of drawing at least N lands by turn N, in decks with 15-19 lands; the first shows the probability on the play, and the second on the draw.
See if you can replicate these numbers with a hypergeometric calculator! Population size is always 40, sample size is the number of cards you see by turn N (6+N on the play, 7+N on the draw), successes in population is # of lands in deck (15-19), and successes in sample is just N. Since we want to check for when we make our Nth land drop, we're looking for the probability that we've drawn at least N lands, so P(X≥x).
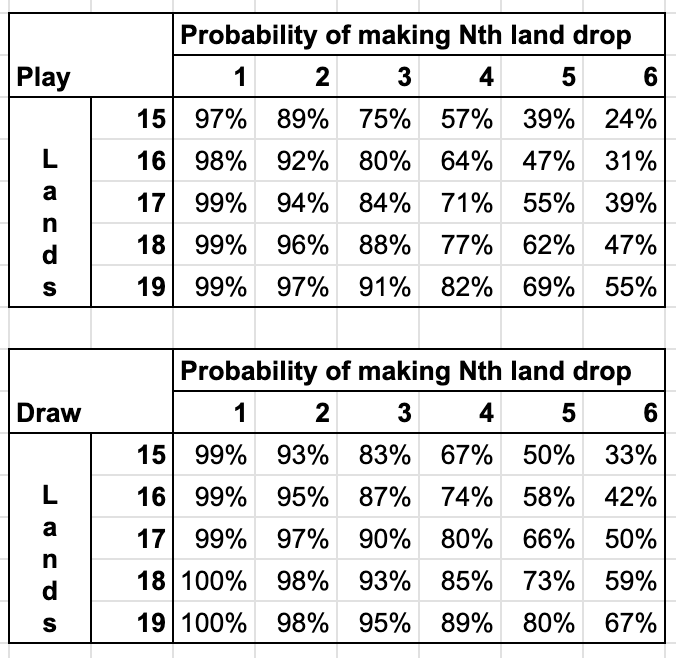
land drop chart; rounded to nearest %
Here, we can start to see why 17 lands is the standard. Most limited decks really want to hit their 3rd land drop on time, and somewhat care about their 4th as well, especially for the purposes of double-spelling.
At 16 lands, you have a 20% chance (one in five!) of missing your third land drop on the play, and a 36% chance (more than one in three!) of missing your fourth!
Those numbers are quite substantial - and by just going up one more land, you reduce them to 16% to miss your third land drop (one in six) and 29% (a bit more than one in four) to miss your fourth.
Of course, we could just keep going higher and higher in land count, making our land drops more and more likely. This mana screw analysis naturally only tells us the downsides of playing fewer lands, and not the downsides of playing more. For that, we turn to:
Part 3: Calculating Flood
It's a lot harder to calculate the effects of flood. For one thing, by the time flood starts mattering, it will naturally be later in the game, and thus more things will have occurred that could throw off simple models like the one we're using.
We've been assuming that you see no more cards than the ones you draw for turn. And while this is true in the opening turns of the game, this is very much not the case as the game goes on. Many tools for flood protection exist, ranging from scrying to rummaging to card draw.
But still, let's do our best to try to quantify this a bit. It'll be a lot more rough estimation than solid calculation, but we can probably still glean some useful information.
First of all, take a look at this graph from 17lands. This shows how long games last on average in each format, and how that correlates with winrate on the play.
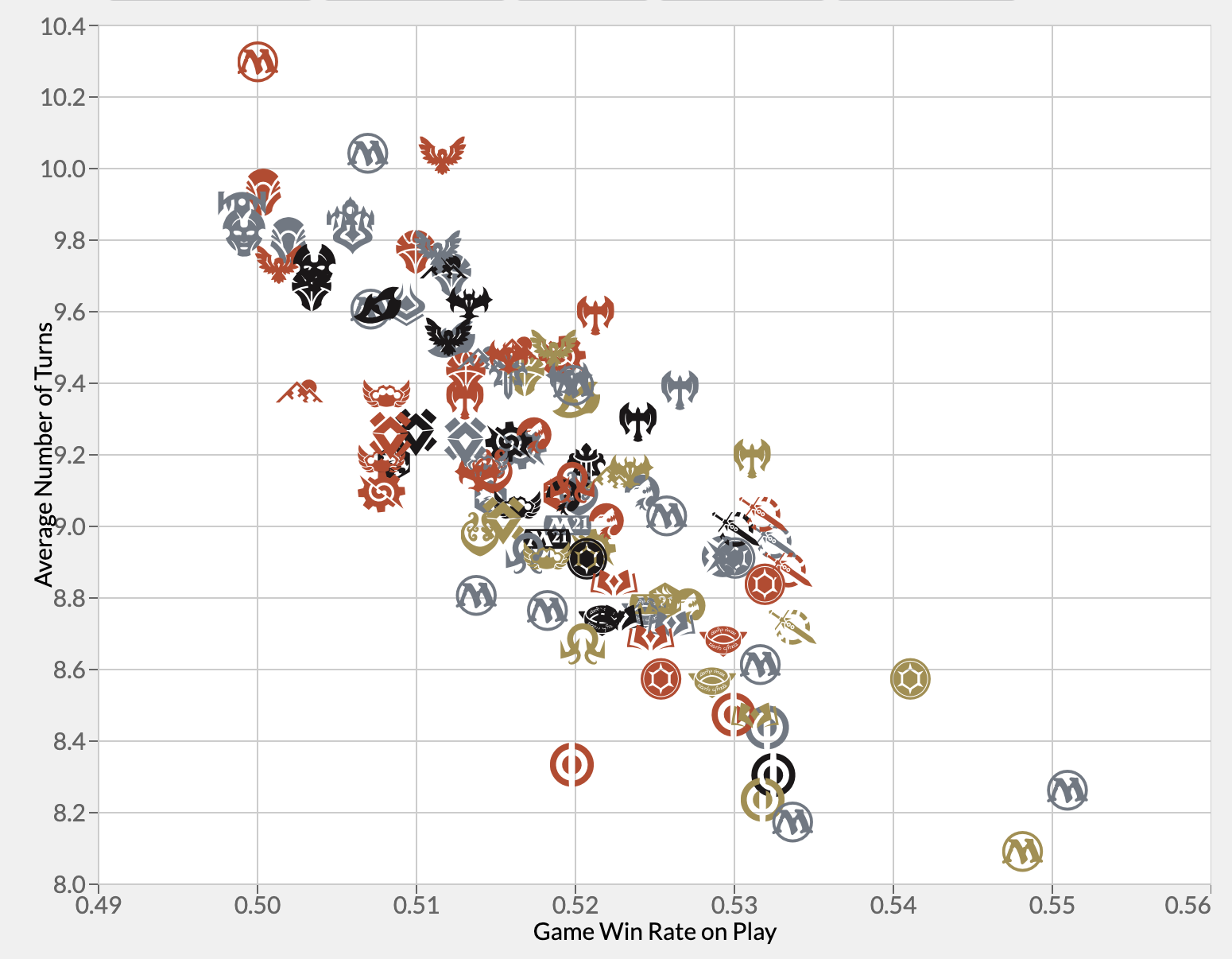
format speed graph from 17lands
As you can see, while there is some amount of variation, with a range from about 8-10 turns, most formats will have games that last about 9 turns on average.
So how can we use this for our simple model? Well, if games last about 9 turns on average, that seems like as good of a place as any to set a benchmark. And for our benchmark, let's pick something simple, if a bit arbitrary: what's the probability that, by turn 9, we draw at least 9 spells, for an average of one per turn?
Obviously, double spelling is quite important in limited. But between activated abilities, mechanical flood insurance like adventures, and the fact that 1-drops are fairly uncommon, I think it averages out such that this is an okay benchmark.
So, again, here's a chart with the numbers. This time, I've assumed that you, in some fashion, get to see 2 more cards than normal over the course of 9 turns - whether through something like a Divination, a Tormenting Voice, a scry 2, or something else. This adds up to 17 cards on the play, and 18 cards on the draw.
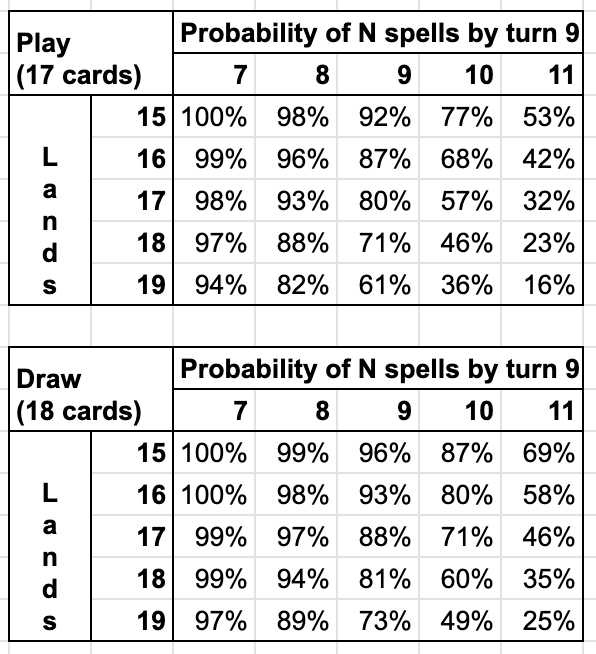
chart depicting probability of drawing N spells; rounded to nearest %
I've included the probabilities for 7-11 spells, not just 9. And again, we can see 17 lands standing out as the gold standard.
At 18 lands 22 spells, we have a 29% chance (more than one in four!) of drawing fewer than one spell a turn by turn 9 - and going to 17 lands 23 spells shifts that to down to 20%, or one in five.
And, as with the mana screw calculation, of course going further in that direction helps more - but it seems that 17 lands just happens to be at the intersection of reasonableness! 80% to hit your fourth land drop on the draw, and 80% to draw 9 spells by turn 9 on the play.
Part 4: Vibes
At the start of all of this, I kind of misled you. I started with the question: "How can we know that 17 is generally the right number, and how can we know when it isn't?" But in reality, we can't really know for sure - none of these calculations have been super rigorous, as there have been many assumptions and approximations.
Why do I care about having 80% to hit your fourth land drop on the draw? Why do I care about being 80% to draw 9 spells by turn 9 (assuming 17 cards seen)? Why am I assuming you see ~2 more cards in those 9 turns?
I can't point to a reason for these numbers a priori, but from experience I can say that they just feel like the right standards to set. This is also why I don't care too much about the inaccuracies of this simplified model - I'm going off vibes anyways, I don't need anything super accurate.
But even with this being so imprecise, it is still a very useful process to think through. I may not be able to tell you exact numbers, but I can show you how different numbers of lands roughly shape the chances of making your Nth land drop and the chances of flooding. I can't make a perfect algorithm, but I can present something a bit more useful and reasoned than "just play 17".
I could imagine a limited set that differs enough that you care so much more about hitting your sixth land drop than flooding out, or one where flood is your main way of losing and you can function on two lands. But it turns out, at their core, a lot of limited sets are quite similar. And while they stick to that core, 17 lands will continue to be the standard.
Part 5: Nuance
Of course, all of this has just been about finding a standard. And standards are made to be broken! So when should you break this one?
Well, maybe you don't care about your third and fourth land drops. Most limited decks can't function purely on two lands, but some aggressive, low-curve decks can get away with it. If you're fine missing your third land for one or two turns, and are much more worried about flooding, consider cutting lands.
Even 15 lands has a three in four chance of hitting the third land drop on the play, and while that's a lot lower than most decks want, that can certainly work for some!
On the flip side, maybe you care a lot about your fifth and sixth lands! A 17 land deck is only barely above 50% to hit its fifth land drop - additional mana sources or card draw can help this. And if you can either function with fewer spells or have more ways to see more spells, you can effectively mitigate the flood risk.
If you do decide to deviate, though, consider plugging a few numbers into the calculator, and checking that you're actually okay with those odds.
#FreePalestine | Consider donating to UNWRA or PCRF, supporting protesters locally, and educating yourself.
